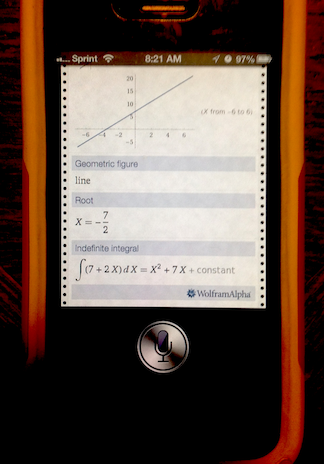
 “Siri, can you tell me what 2x+7 is?”
“Siri, can you tell me what 2x+7 is?”
You know the future is rushing towards us when students no longer ask the teacher if they can use a calculator, but instead ask if they can ask Siri. Yes, that iPhone phenom with the sort-of-sultry voice.
When I asked Siri, I didn’t just get the answer to my query.
Siri shows me a plot of the equation, what kind of geometric shape it is, and loads of other things that are well above the needs of my 8th graders. I thought the image on my screen looked remarkably like the data one finds at the Wolfram Alpha site. And sure enough, Wolfram is built right into the Siri help menu.
Amazing.
Asking your smartphone to answer questions for you in school is not something I’ve anticipated. I had to stop and think about it for a bit. Clearly it won’t take long for my students to realize how easy this is to access. In a year’s time they’ll likely be well entrenched in using Siri or some Siri surrogate to find the answers to math problems and potentially lots of questions in other subjects.
How will and should my teaching change?
Short of banning smartphones (a short-term solution, at best), I think the evolution of AI services like Siri means that the problems I pose for my students will have to shift from a focus on finding the answer as the endpoint — to a greater focus on analysis. OK, you have the answer but so what? What does that answer mean in a real-life situation?
One of the things I’ll need to consider is how to use all that information that Siri returns. Should I just take the bit that I have traditionally needed for this kind of problem? OR should I figure out how to use this extra information provided by Siri to push their thinking beyond where we usually go with 8th graders?
 Taking digital tools and mobile technologies into account (not to mention Common Core expectations) , it’s obvious that multiple-choice and true-false questions are not going to cut it anymore. Instead I have to design questions that force students into drawing conclusions and using the proof process that many of them haven’t encountered yet.
Taking digital tools and mobile technologies into account (not to mention Common Core expectations) , it’s obvious that multiple-choice and true-false questions are not going to cut it anymore. Instead I have to design questions that force students into drawing conclusions and using the proof process that many of them haven’t encountered yet.
I’m already doing some of this
I’ve already done a bit of this expanded kind of problem-solving using challenge questions. I give them both the question and the answer and their task is to explain how you solve the problem — how you harvest the information from the problem and show the steps in the solution. This way it’s clearly NOT about “getting the right answer.”
Here’s an example: Instead of reviewing the commutative and distributive properties with a worksheet where they would be able to enter the equation into Siri and get the answer, you ask the question in a different way. You can ask them…”Is 5(5x+7) = 25x+7 always, sometimes or never true?” Or you might ask “Is 3x-9 = 9-3x always, sometimes or never true?”
In the first example, they simply have to answer the question and Siri can help them find the answer pretty quickly. In the second example, students have to test out their idea with different kinds of numbers; positive, negative, fractions, improper, zero and big numbers. They search for an example that proves the equation true, or they search for a counter-example that proves what they conjecture to be false.
It’s a balancing act
Changing instruction in this way is a balancing act. I’m looking for ways to design lessons that (a) assume students will use readily available technology, and also (b) tie any assignment I give them to prior knowledge so the learning will stick.
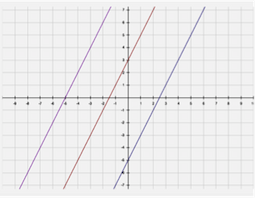 For example, when we study parallel and perpendicular lines, the objective is for students to learn how the coefficients of these lines are the same and how they are different. It’s easy to give them a definition to memorize but will they remember it? I have to hook the idea to something tangible that they’ve done if I hope to give them this learning for life.
For example, when we study parallel and perpendicular lines, the objective is for students to learn how the coefficients of these lines are the same and how they are different. It’s easy to give them a definition to memorize but will they remember it? I have to hook the idea to something tangible that they’ve done if I hope to give them this learning for life.
Many of my students have already downloaded free phone apps for a graphing calculator and use it regularly. They even send me screenshots to show what they’re thinking or where they are stuck on a problem. They’ve begun to do this because they see me using the graphing calculator, Geometers Sketchpad, and similar digital tools all the time.
As a result, I’ve adjusted my instruction around the assumption that we use these digital tools just as we use pencils and notebooks. And graph paper!
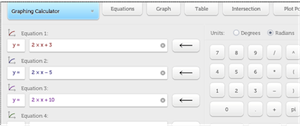 When we studied parallel lines, I used a graphing calculator application to show different lines. It was easy for students to see the graph and equation of many lines. They quickly found the pattern of all lines having the same coefficient. From seeing this and using their smartphone app to test out different equations to see if they still are parallel, students “do” the learning and combine it with memorizing the definition. Doing both things cements the definition and the working knowledge together.
When we studied parallel lines, I used a graphing calculator application to show different lines. It was easy for students to see the graph and equation of many lines. They quickly found the pattern of all lines having the same coefficient. From seeing this and using their smartphone app to test out different equations to see if they still are parallel, students “do” the learning and combine it with memorizing the definition. Doing both things cements the definition and the working knowledge together.
Another example: Estimation
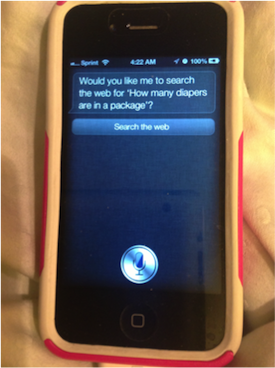 Students just worked on another kind of problem where Siri played a big role — estimation. We’re using the Estimation 180 website where I’m trying to expand students’ number sense and ability to use context clues to estimate mathematical kinds of answers.
Students just worked on another kind of problem where Siri played a big role — estimation. We’re using the Estimation 180 website where I’m trying to expand students’ number sense and ability to use context clues to estimate mathematical kinds of answers.
The problem that we tackled was to estimate how many diapers were in a large shipping package. Quickly, students decided the way to answer this question was to ask Siri.
I was nervous they’d find the answer and be done. Fortunately, she couldn’t immediately give them the answer.
Siri did come back and offer to search the web for them and that took them to the Huggies website where they found out that not all diapers are the same size. That led students to ask more in-depth questions about size, dimensions and how many diapers come in a typical box you buy at the store…all of which eventually developed into a pretty good estimation.
Implications for other subjects
If I’m seeing these conversations between students and their phones in math class, Siri is helping students in other classes too. She’s very capable of finding the capitol of a state, the 22nd president of the USA, and who wrote the phrase “Four score and seven years ago.” She knows the plot of every book in the Google Library and won’t hesitate to define “iambic pentameter.” Chemical symbols? Physical laws? A snap.
I wonder how other teachers might have to rethink their teaching and assessment strategies — with Siri and her AI colleagues at our students’ beck and call?
Marsha Ratzel
Latest posts by Marsha Ratzel (see all)
- Scaffolding Quadratics: 2 Things My 8th Graders Taught Me with Student Feedback - May 20, 2019
- Student-Driven Common Core Classrooms - February 14, 2013
- Shifting toward PBL in Math - December 6, 2012


Wow, this post really got me thinking. What does this kind of environment mean for any kind of teaching and learning? Are we paying enough attention to how the technology, and this is just one example, needs to make educators think about whether we are really ready for what the technology forebodes, and I use that word “forebodes” loosely? Perhaps this kind of technology will prompt us to not only re-think hackneyed teaching methods, but also consider our preparation for here and now and the future. Yet how to we prepare for this transformation? What philosophical approaches to teaching and learning are best suited for the information technologies available now and in the near future?
Judy, I have been thinking a lot about exactly that recently. We have experienced a MAJOR shift via technology whereby any piece of information you want to know or any specific skill you need to learn is literally available at your fingertips. My daughter recently learned how to do vibrato on the violin by watching and re-watching a video on YouTube; but her love for and appreciation of the instrument and its music she got from her teacher.
Policymakers continue to be obsessed with “achievement”–how much ‘stuff’ has the student “learned”? They are obsessed with content, when (specific) content is really secondary in some respects.
What schools should be focusing on, what students need to learn are habits of mind–problem-solving, analytical thinking, empathy, and so on along with the ability to learn and a passion for learning. There is no age limit for learning things off the Internet (or elsewhere); and more free courses pop up every day. But students need to have the learning skills and habits of mind in place in order to take advantage of those opportunities. Askng Siri what 7x+1 is will show them a lot; but if they just passively read it and go on, they haven’t leaned very much.
Students should be thought of as learner apprentices; and EVERY child should have the right to study the important things mentioned above with a master educator in a fully-resourced learning environment for the dozen or so years s/he is in school.
Dear MRM,
Thanks for posting your ideas. I’ve had those very thoughts myself and it’s a delicate balance to move forward and still retain the best of our educational system.
I love your statement, “Students should be thought of as learner apprentices; and EVERY child should have the right to study the important things”. That’s so true.
It’s exactly why I had to stop and wonder and ponder ….what should be my response to this kind of student use of technology. Should I forbid it? Should I replace my instruction with it?
To both of those questions, I concluded “no”. Instead I see that my learner apprentices need to know how to use the information in their discussions and considerations. Sure this generation can search to find answers. But once they find an “answer”, they need a classroom, a teacher and a community with which to discuss the meaning of what they found.
It’s the meaning making process where the learning takes place. Not in discovering that Siri can find the answer.
I hope that makes sense.
Oh my gosh Judy…..you’ve got a whole conversation of questions in your comment.
It is foreboding….but hopefully in a good way. I think we first raise awareness and then consider what it means. hopefully not taking too long so we can really be proactive in designing learning in different ways.
How do you think we start to shift our philosophy of teaching and instructional toolchest?
Marsha, I just hope you can get other educators into the conversation. I am curious about what others think given this technology at the hands of students and teachers. This summer, I used Siri to get me all over Hawaii. It is also amazing to see how the device can not only talk to you, but also supply the visuals. We are seeing both voice activated response as well as the answers spelled out (or enumerated, diagrammed, etc.) right before our eyes. It is as though science fiction is not fiction but reality. This kind of technology is already being used during surgical procedures–yes, I am not kidding. Surgeons can pose a question and get a quick oral response with video while they are in the operating room.
It sounds alot like glgooe TV but like all things apple will sell better and be better.Also I want to know if it will be like the iPhone was in the rest of the world they are open to all networks from day one so not locked in to cable company’s, as cables not as highly used out side the USA
Dear Judy,
Thanks for your second reply. I hear you….and I think your Hawaii trip is a perfect example.
I guess what surprised me is this….I am a big Siri user in my personal life. Somehow that kind of use didn’t make me aware that it had impact on my professional life. I had a serious disconnect between what I do for me and what I was doing as a teacher.
Realizing I had a gap, sounded the gong of awareness for me that I needed to start thinking about this. Sooner rather than later.
I think you might be right…it’s not only the answer that you can get the multiple representations of that answer. Wonder if that’s my entry point into considering how I should think about changing my practices?
Interesting though, and probably relevant, that Siri could not give the answer of “an expression”.
Yes, we need to change our focus, but not just to analyzing answers Siri gives us. We also need to ask the questions that Siri can’t answer.
Dear KW,
Changing focus is what we’re already doing, in part as a response to CCSS, but also to just be using best mathematical practices in our classrooms. It aligns with so much of what I see people like Dan Meyer doing with his story problems work.
But I’m not sure I think we need to always ask questions that Siri can’t answer. In my class, those questions are the building blocks. Without understanding those computational kinds of things, students can’t test out their ideas, conjectures or wonderings.
I’m convinced it’s in building the culture of wondering, of playing around to see “what happens when….” Experimenting with math ideas. It’s also, for me, learning to have conversations that rely on students supporting their ideas with proof.
Thanks KW for posting.
Thank you so much for this! We are now starting to have these conversations at our school because of your information. Thank you for all of the replies as well. Very good discussion.
Dear Belia,
That’s such encouraging news…where will your school start in considering these issues? I know that the BYOD (bring your own device) policies can either encourage cellphone use or even prohibit it.
Do the policies of your school allows students to bring and use a cellphone to class?
Thanks for posting your idea and I appreciate it.
Marsha,
As ever, when I read your stuff, I walk around for days with the cogs turning in my brain, thinking and rethinking. I’ve been fascinated by my own boys’ response to a friend’s Siri-equipped device. They love it – love trying to stump it, love seeing what it will do, and where it will take them. I think the thing that most struck me about your post, though, was the obvious understanding in your classroom that your students’ personal devices are welcome there. You weren’t penalizing your students for using Siri – instead you were figuring out what needed to change to make room for her. That’s still what I find I’m running up against in the educational establishment.
Judy, I loved your “science-fiction-y” experience. Yesterday, while watching some of the Apple launch with a handful of students during lunch break, I told them that these products ALL make me feel like I’m living in an episode of Star Trek.
Dear Lisa,
Thanks for posting your comment… I think the story of your boys’interest in stumping Siri is “right on”. I am used to thinking about a device as something I use for enjoyment (thinking of a DVD player) but now I can also use it for learning (thinking of not only watching my favorite Cary Grant movie but also watching re-runs of the Presidential debates and using it to teach persuasion techniques in an ELA class).
I know this is a very cliche statement, but it’s easy to forget what a powerful computer lies at the heart of a smartphone. More powerful than anything that was in my school computer labs just 15 short years ago. I think I need to re-connect.
I thought the same thing about the mini. I can hardly wait for a tricorder or to use the Universal Translator!!!!
I’ve read this article twice. It specifically discusses the use of Siri in classroom instruction (and by inference homework). It does not mention assessment/testing. Will smartphone Siri use be allowed during a test (in whatever subject) at any grade level?
As a matter of pedagogical principle, academic excellence and self-respect, ought an 8th grade or older student – without using either Siri or a calculator or even pencil and paper – be able to solely look at an equation such as 2x + 1 = 3 and, using only “zee leetle gray cells” (Agatha Christie’s “Poirot”), figure out quickly that x = 1?
The same for 1/2 + 1/4 = 3/4, or 1/3 + 1/2 = 5/6?
Too many students take time they don’t have during a test to input fractions into a calculator. They get an answer but if they can’t independently calculate a common denominator (when adding or subtracting) to check their answer, then the only skill they are demonstrating is that of carefully pushing buttons in the correct memorized sequence.
Regarding higher level high school algebra, how about a test question like, “Solve for x in (x)(x) = x + x”? Again, can one consult Siri during a test? This is simple enough that “by inspection” – looking at it – or a little bit of trial-and-error, a student can see that x can be both 2 and 0. But what if he is required to algebraically show how he got the answer?
If a calculator is allowed, are we going to be satisfied with a student inputting that equation on a graphing calculator, and then consulting the table to decipher the answer?
[It will have to occur to the student to enter it as
y = (x)(x)-2x, at the same time comprehending that (x)(x) – 2x = 0 = y.]
Is that good enough? Or does he need to show his work by using the quadratic formula (a star in his crown if he can show how it is derived from y = ax^2 + bx + c), or by “completing the square”?
Dear Filippo,
Thanks so much for reading this post and responding with loads of terrific questions. You raise any number of valid concerns and things that every math teacher must decide.
How many decades have we been wrestling with whether or not a student should use a calculator? Mostly for the reasons you mentioned and I would imagine that teachers have considered how to balance using a tool that assists a student in getting an answer with understanding the concepts behind the answer. To be able to use a tool without understanding doesn’t free the student to think bigger, more analytically or use it well. It handicaps them.
But I also see that denying that, when our students graduate and become engineers, architects and accountants, they won’t embrace Excel, other software programs and calculators to do the number crunching isn’t helpful either.
I think I’m advocating for a middle ground approach here. I see a place for using any kind of tool (graphing calculators, Siri, Excel and so on). In my mind, it shouldn’t be a replacement for understanding. So where does that leave me as a teacher?
I believe a teacher should use their expertise in gauging whether students have the understanding foundation. Can they “get” the answer in a way that shows their understanding of the ideas and the procedure? If they can, then let’s move on…using that idea/procedure and applying it to a real life examples and problems. It’s where my professional knowledge really kicks in…and where I’m able to tell the difference in these two kinds of understanding.
It’s where I take those learner apprentices you mentioned to new places that we couldn’t go when we were still number crunching with pencil and paper. And it’s where mathematical ideas are tested, explored and unleashed.
Marsha,
What a wonderful article! We haven’t chatted in ages – but I used to teach at Prairie Star Elementary. 🙂 You were a lifesaver in helping me learn to integrate technology into my third grade classroom – especially iMovie. Thanks much for your continued visionary work, and congrats!
Hi Kari,
It’s great to hear from you….I definitely remember you. We had a blast and at a time when SmartBoards were so new. I remember that your students were so small that they had trouble reaching the board. I can’t remember…did they build a platform for them or did they lower the placement of the board.
So what do you think about AI like Siri? How do you see it will change our instructional strategies and pedagogies?
Wow, this information was pretty interesting. I never thought of using Siri in the classroom with the students. I know this will help motivate students to learn. I am only hesitant about this idea because I wouldn’t want my students to become dependent on the device. I would also want them to solve problems on their own. I think that with the proper teaching techniques on this device, then will will help students thrive.
Dear DebbyO,
That was what shocked me too….my students were using their phone to record their HW and we’d used them to some of those phone-based surveys and even downloaded apps for graphing calculators. But I’d never expected them to start using Siri as a classroom tool.
But now that it’s happened, I guess I think…why not?
I want students to problem solve too. But in this day and age, I think more students are searchers for information than producers. Somehow we have to figure out how to blend the best of being a searching and a problem solver….banning the search implement won’t stop them from being this way. It only postpones what we must and should address.
Not something that is easily considered. I’m glad I posted this because I think it will be something we all have to craft together.
I agree with you Marsha, that it will be important to blend searching for answers and solving for answers. Due to the fact that we are in the digital age using tools like Siri in the classroom will be helpful, as well as, necessary to an extend because without utilizing technology like Siri we doom are classes and students to be stuck in the “Stone-Age”. That being said, knowing how to solve equations will remain a requirement when teaching because without the how and why than the answers may lose relevancy.
Dear My-Hoang,
You said, “That being said, knowing how to solve equations will remain a requirement when teaching because without the how and why than the answers may lose relevancy.”
To my mind’s eye, that is the essence of the teacher’s role in this new kind of classroom. Through our teacher’s expertise, we must balance what our students “like” to do with what we see is in their best educational interest. I would imagine a mathematical conversation where the searched&found content is blended into student understanding.
Don’t you think that the other piece to this will be understanding what to keep and believe when they search? Without understanding the idea, finding just any old thing will be enough. But it isn’t. I’m beginning to realize that it’s another form of literacy….recognizing that what they’ve found is useful to them in performing/completing their study of a math concept. And what’s a bunch of bunk.
Thanks for posting and bringing up this excellent point. Do you see this as how teachers will address the concern you mentioned?
Great post! I totally agree with you!
The answer is not the product (for any discipline). The answer is just part of the process. The product is the knowledge that the students walk away with.